判断某个点是否在矩形范围内

pre

• 一个业务需求，45°俯视角的游戏场景如果用正方向矩形拉范围视觉上是个菱形
• 这时候需要用到45°矩形
  

判断某个点是否在矩形内

struct point {
    int x = -1;
    int y = -1;
};

正方向矩形

• 需要2个point: left_top 和 right_down
• 只需要检查目标点 pt

  pt.x >= left_top.x && pt.y >= left_top.y
      && pt.x <= right_down.x && pt.y <= right_down.y

方向矩形

• https://math.stackexchange.com/questions/190111/how-to-check-if-a-point-is-inside-a-rectangle/190373#190373
• 靠前的回答：

  M of coordinates (x,y) is inside the rectangle iff
  
  (0 < AM ⋅ AB < AB ⋅ AB) ∧ (0 < AM ⋅ AD < AD ⋅ AD)
  
  (scalar products of vectors, ∧ stands for logical AND).

画图理解：

• 假设是正方向的矩形
  

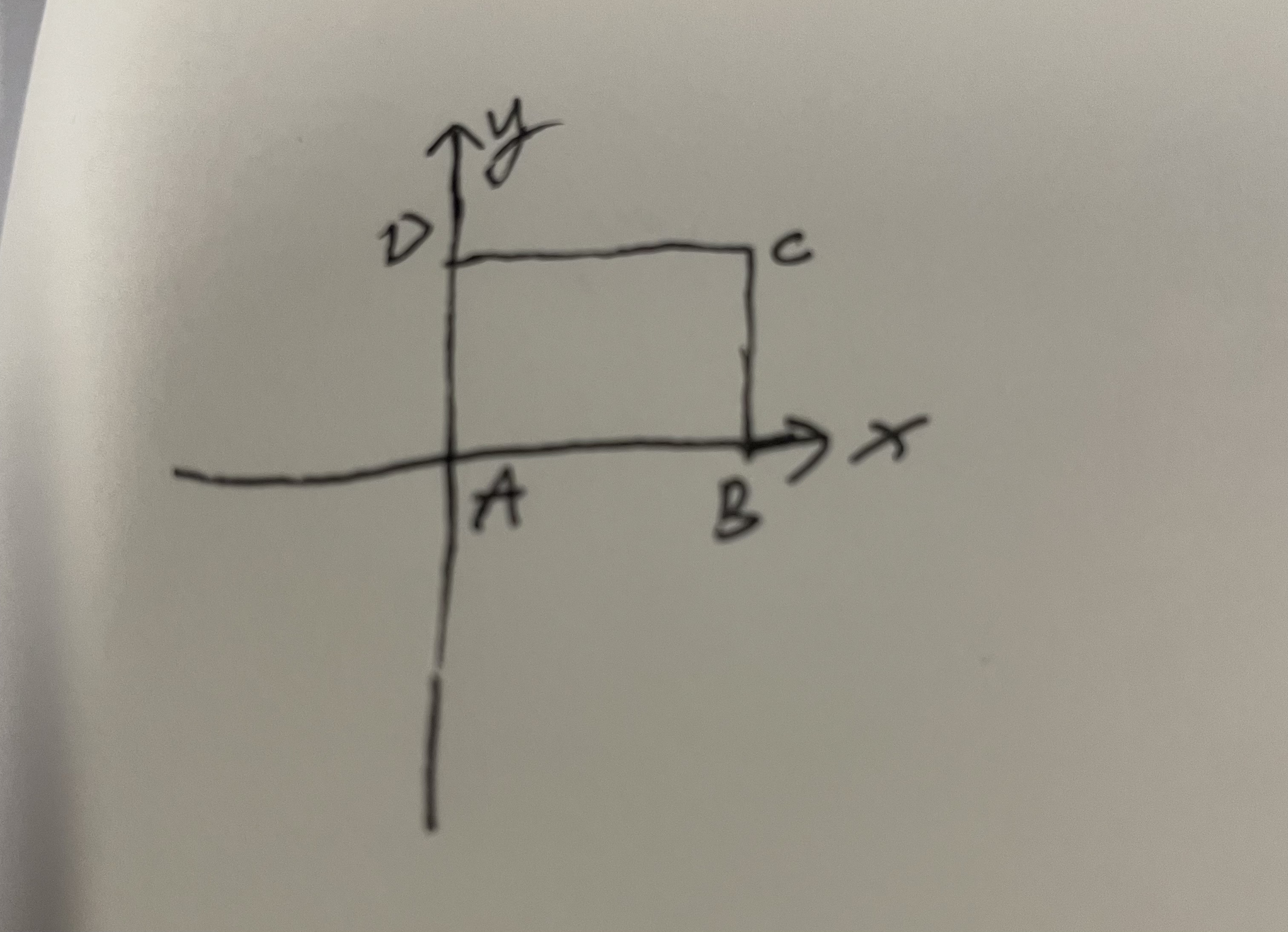
• 贯穿全文的公式：

  • 向量 a ⋅ b = |a|*|b|*cos(角度)

• cos(角度) 对应值：
  

• 公式里两个 > 0 的是由 cos 的正负决定的

  • AM ⋅ AB >= 0 表示点在 y 轴左边 （1,2象限）
  • AM ⋅ AD >= 0 表示点在 x 轴上面 （1,3象限）
    
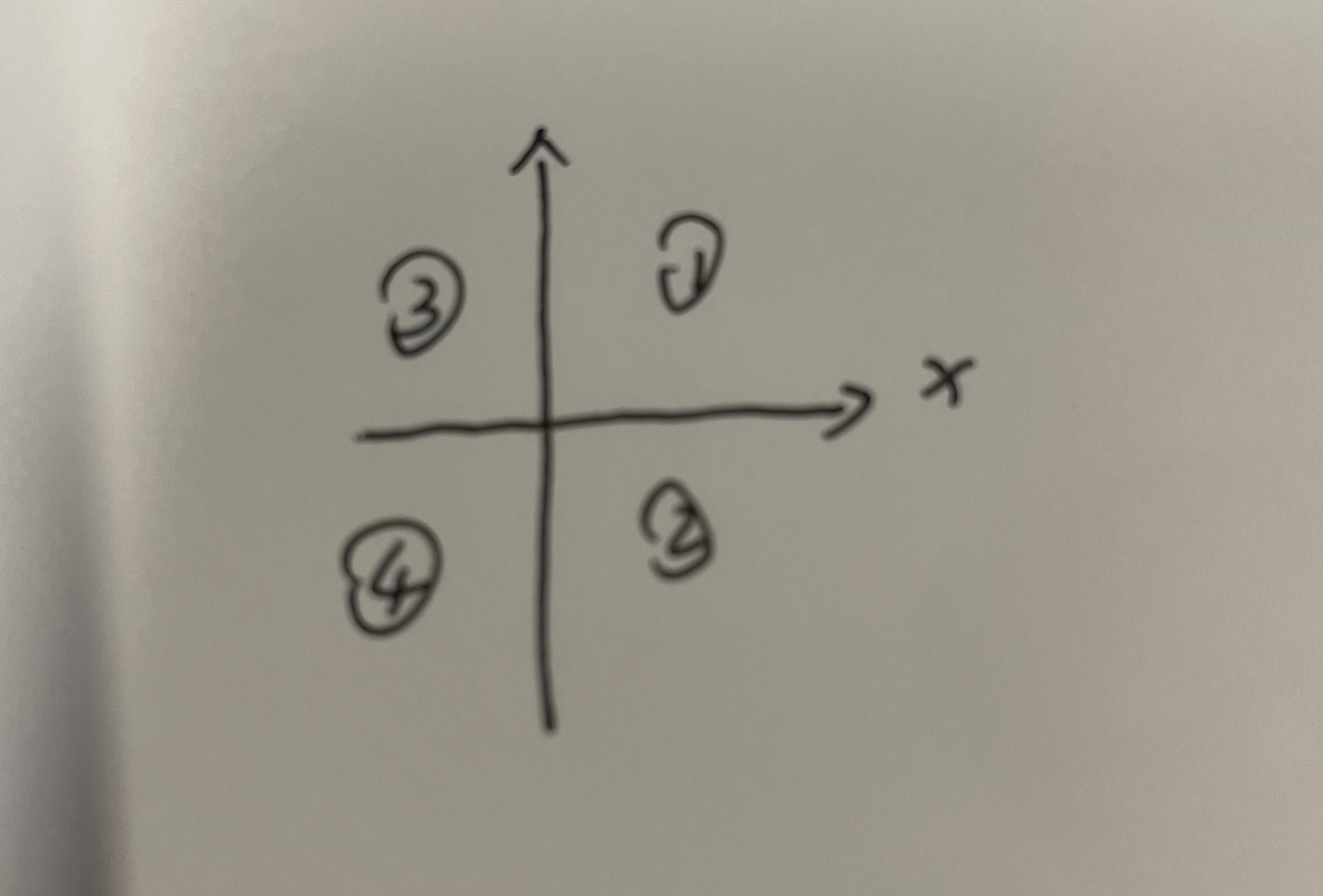
  • 重合的就是 1 象限

• AM ⋅ AB < AB ⋅ AB:

  • AM ⋅ AB = |AM| |AB| cos(角度)
  • AB ⋅ AB = |AB| |AB| cos(0) = |AB| |AB|
  • |AM| |AB| cos(角度) < |AB| |AB| cos(0) 得出
  • |AM| cos(角度) < |AB|

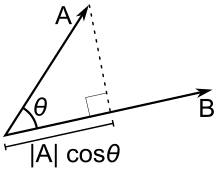
- 图里 A 代表 AM, B 代表 AB

• AM ⋅ AD < AD ⋅ AD 同理

参考

• https://www.jianshu.com/p/bde70668b1bc
• https://math.stackexchange.com/questions/190111/how-to-check-if-a-point-is-inside-a-rectangle/190373#190373
• https://stackoverflow.com/questions/2752725/finding-whether-a-point-lies-inside-a-rectangle-or-not
• https://en.wikipedia.org/wiki/Dot_product